正規分布とは図１のように山型で左右対称な形の分布形状のものを言います。自然界で得られる多くのデータはほぼ正規分布に当てはまります。

取得したデータのバラつきが大きいと山が低くなり、バラつきが小さいと山が高くなります。

バラつきの大きさは標準偏差σで表されます。

図１にあるデータ群Aはバラつきが小さく山が高い。データ群Bはバラつきが大きく山が低い。

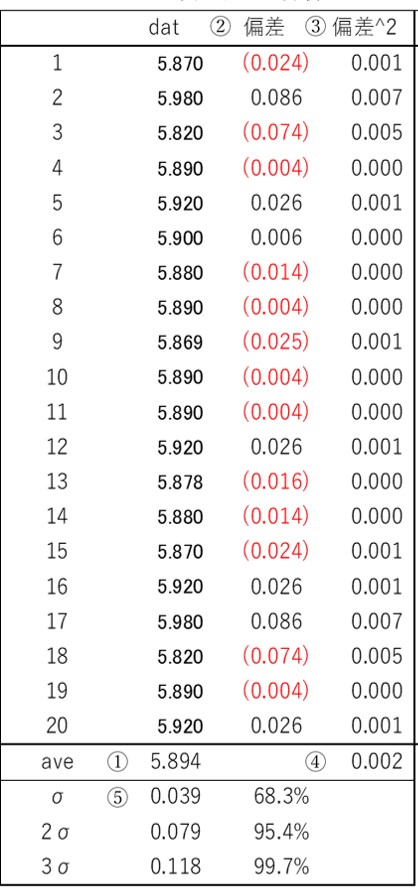
図2に示すように20個のデータ（dat）から標準偏差σを計算する手順を確認します。

①データの平均値を計算します。

②各データと平均値との差を計算します。偏差と言います。

③偏差の2乗を計算します。

④上記③の平均値を計算します。

⑤上記④の平方根（ルート）を計算します。

σを2倍すると2σ

σを3倍すると3σ

・

・

・

となります。

例えばある部品に切削加工を行い、寸法データを取った結果平均値が5.8、標準偏差σが0.05となった場合を考えます。。

このデータの分布からいえることは次の通り。

平均値±σ、つまり5.75～5.85の中にデータが入る確率が68.3％。

平均値±2σ、つまり5.7～5.9　の中にデータが入る確率が95.4％。

平均値±3σ、つまり5.65～5.95の中にデータが入る確率が99.7％。

正規分布を描くには標準偏差σと平均値を計算します。

さて、表にあるデータ（dat）の集まりから標準偏差を求めて正規分布のグラフを書いていきます。

①データの平均値を計算します。

②個別データと平均の差、偏差を計算します。

③偏差の2乗を計算します。

④③の平均値を計算します。

⑤④の平方根を計算します。

⑥確率計算にエクセル関数を使います。

⑦横軸にdat、縦軸に確率密度を取り散布図を書けば完成です。

右の表をグラフ化すると図３の通りになります。