解説：H.sin氏（機械部門）

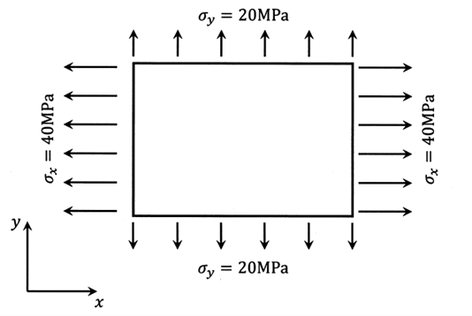
下図に示すように，長方形板のx軸に垂直な面に引張応力σx=40MPaが，ｙ軸に垂直な面に引張応力σy=20MPaが作用している。この板における主せん断応力τの大きさと主せん断応力が作用する面の角度θ（その面の法線ベクトルがx軸となす角度）の組合せとして，適切なものはどれか。

①τ＝±10MPa　θ＝±30°

②τ＝±10MPa　θ＝±45°

③τ＝±√10MPa　θ＝±30°

④τ＝±√10MPa　θ＝±45°

⑤τ＝±20MPa　θ＝±45°

解説

[解くために必要な知識]

　σx,σy，τxy　の力がかかるときの主応力はモール円を書くことで分かる。

σx,τxyの位置とσy,-τxyの位置を線で結び、その線が直径となる円を書く。せん断主応力、最大主応力、最大主応力のなす角はモール円から分かる。

では、問題を解いていきます。

　σx=40MPa

　σy=20MPa

　τxy＝0MPa

上記の３条件から、座標軸（σx,τxy)と(σy,τxy) (40,0)(20,0)の中点(30,0)を中心とした円を書く。円の頂点部がτmaxとなるため、モール円の半径10MPaが主せん断応力となる。

　また，モール円ではｘ軸とτmaxのなす角度2θ＝90°であり、せん断主応力の角度θは45°となる。

よって回答は②となる。

＜前の問題へ　次の問題へ＞

技術士試験対策Topへ戻る

令和4年解答解説へ戻る