解説：H.sin氏（機械部門）

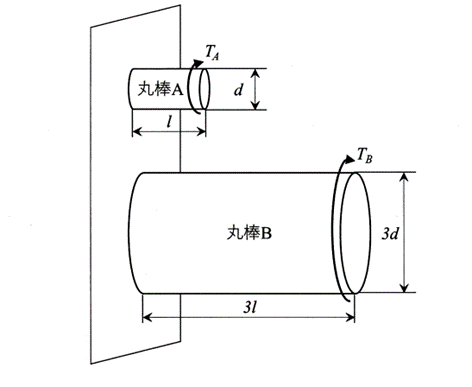
下図に示すように，同一材質の丸棒A（直径d，長さl）と丸棒B（直径3d，長さ3l）の一端が剛体壁に固定され，他端にねじりモーメントTAとTBがそれぞれ作用しているとき，丸棒Aと丸棒Bの両端間のねじれ角が等しくなった。このとき，ねじりモーメントの比TA／TBとして，適切なものがどれか。

①27　②3　③1　④1/3　⑤1/27

解説

[解くために必要な知識]

　ねじれ角θ＝lΔθ＝Tl／GIp

　丸棒のIp=πd4／64

では、問題を解いていきます。

丸棒Aのねじれ角

θA＝TAl/(G・πd4/64）

丸棒Bのねじれ角

θB＝TB(3l)/｛(G・π(3d)4/64｝

θAとθBが同じなので

TAl/(G・πd4/64）＝TB(3l)/｛(G・π(3d)4/64｝

左右の項で同じものを消していくと

TAl/d4=TB3l/(3d)4

さらに式を変形し求めるべきTA/TBの形をつくる。

TA/TB=3/34= 1/27

よって回答は⑤となる。

＜前の問題へ　次の問題へ＞

技術士試験対策Topへ戻る

令和4年解答解説へ戻る