解説：H.sin氏（機械部門）

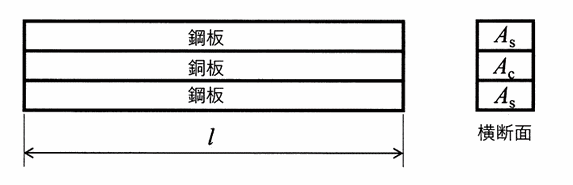
下図に示すように，2枚の鋼板の間に銅板を接着した。このとき積層板に応力は発生していない。鋼板と銅板それぞれの横断面積をAs，Ac，縦弾性係数をEs，Ec，線膨張係数をαs，αcとし，αs＜αcとする。積層板の温度をΔTだけ上昇させたとき，鋼板に生じる熱応力σsと銅板に生じるσcの組合せとして適切なものはどれか。

①σs=2(αc-αs)EcEsAc／（2EsAs+EcAc）×ΔT

　σc=-4(αc-αs)EcEsAs／（2EsAs+EcAc）×ΔT

②σs=2(αc-αs)EcEsAc／（2EsAs+EcAc）×ΔT

　σc=-(αc-αs)EcEsAs／（2EsAs+EcAc）×ΔT

③σs=(αc-αs)EcEsAc／（2EsAs+EcAc）×ΔT

　σc=-(αc-αs)EcEsAs／（2EsAs+EcAc）×ΔT

④σs=(αc-αs)EcEsAc／2（2EsAs+EcAc）×ΔT

　σc=-(αc-αs)EcEsAs／（2EsAs+EcAc）×ΔT

⑤σs=(αc-αs)EcEsAc／（2EsAs+EcAc）×ΔT

　σc=-2(αc-αs)EcEsAs／（2EsAs+EcAc）×ΔT

解説

[解くために必要な知識]

　線膨張係数αと膨張量の関係

ΔL／L＝αΔT　より　膨張量　ΔL＝LαΔT　

では、問題を解いていきます。

　鋼板と銅板が接合されていない場合を想定します。温度ΔT上昇したとき、αs＜αcより、銅板の方がよく延びた状態になります。

実際には、銅板と鋼板は接合されているので同じ長さになろうとする力が働く。

鋼板を引張る力をRs、銅版を引張る力をRcとする。力のつり合いより

Rs+Rc+Rs=2Rs+Rc=0

Rc=-2Rs

　次に熱と力による伸びをそれぞれ求める。

ΔLs1=RsL/AsEs　　(力Rsによる鋼板の延び）

ΔLs2=LαsΔT 　(熱による鋼板の延び)

ΔLc1=RcL/AsEs　＝-2RcL/AcEc　(力Rcによる銅板の延び）

ΔLc2=LαcΔT 　(熱による銅板の延び)

鋼板と銅板は同じ長さになるため

ΔLs1＋ΔLs2=ΔLc1＋ΔLc2

各延びを代入すると

RsL/AsEs　＋　LαsΔT ＝-2RcL/AcEc　＋　LαcΔT 

Rs（L/AsEs　＋　2RcL/AcEc）＝LαcΔT - LαsΔT

Rs=(αc-αs)ΔT｛（AsEsAcEc）／（2AcEc+AsCs）｝

応力は荷重／断面積のため鋼板１枚について考える

σs=Rs／As　

σs=(αc-αs)EcEsAc／（2EsAs+EcAc）×ΔT

RcはRsとの関係より

Rc=-2Rs

σc=-2Rs／Acより

σc=-2(αc-αs)EcEsAs／（2EsAs+EcAc）×ΔT

よって回答は⑤となります//

＜前の問題へ　次の問題へ＞

技術士試験対策Topへ戻る

令和4年解答解説へ戻る