図に示すように、角度θで剛体壁に取り付けられた2本の棒からなるトラス構造において、接点Oに下向きの荷重Pが作用し、破線のように変形した場合を考える。各接点は滑節で、棒の自重は無視できるものとするとき、接点Oの下向きの微小変位δとして、適切なものはどれか。ただし、棒の断面積をA、縦弾性係数をEとする。

 

 

 

解答

③

 

解説

［解くために必要な知識］

全く同じ問題が令和1年に出題されています。（令和1年Ⅲ-2） 

 

ウィリオの作図法を使います。ウィリオの作図法とは、次の手順で変位を求めるものです。

まず2本の棒材が滑節（ピン結合）で図3.1に示すように壁面に固定されていてO点に鉛直下向きの荷重Pがかかっている場合を考えます。

 

このときO点の移動先O‘を求める手順は次の通りです。

　　①部材1の伸び、δ1を求める。

　　②部材2の伸びδ2を求める。

　　③O点から部材1がδ1延びた先を描く。

　　④上記③の先端から９０°の線を描く。

　　⑤O点から部材２がδ２延びた先を描く。

　　⑥上記⑤の先端から９０°の線を描く。

　　⑦上記④と⑥の交点がO点の移動先O’となる。

 

では問題を解いていきます。

 

 

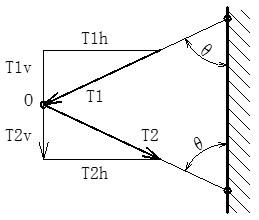
　上側の棒を1、下側の棒を2とします。Pを作用させたとき、図3.2に示すように棒1に生じる張力をT1、棒2に生じ圧縮力をT2とします。それぞれを水平方向hと鉛直方向vの成分に分解します。　

◆まず水平方向および鉛直方向の力の釣り合いを考えます。

＊水平方向は左向きを＋鉛直方向は下向きを＋とします。 

水平方向　T_1h-T_2h=0    (1)

鉛直方向　T_1v+T_2v=P 　 (2)

 

◆次に各分力を求めます。

 

　水平方向

　　T_1h=T₁sinθ

　　T_2h=T₂sinθ

この2式と(1)式から次の関係が得られます。

　　T₁＝T₂ 　　　　　　　(3)

 

　鉛直方向

　　T_1v=T₁cosθ

　　T_2v=T₂cosθ

この2式と(2)(3)式から次の関係が得られます。

　　P=2Tcosθ　

　　T=P/2cosθ　　　　　(4)

 

◆さらに各棒の伸びを求めます。

　棒1の長さL₁=L/siinθ　(5)

　棒1の伸びδ₁=TL₁/AE　(6)

　(4)、(5)式を(6)式に代入します。

　　δ₁=PL/(2AEsinθcosθ) 

 

ここで、図3.3に示すようにウィリオの作図法からδとδ₁には次の関係があります。

　　δ=δ₁/cosθ

　　δ=PL/(2AEsinθcos²θ)　　//

 

 

＜前の問題へ　次の問題へ＞

 

技術士試験対策Topへ戻る

 

 

令和3年解答解説へ戻る