次の記述の［　　　］に入る語句の組合せとして、最も適切なものはどれか。

 

温度境界層厚さと速度境界層厚さの比は［　ア　］に依存する。

熱伝達率の無次元数は［　イ　］であり、強制対流の場合は一般に［　ア　］と［　ウ　］の関数で表される。

　垂直におかれた加熱板上の自然対流では局所［　エ　］が10⁹以上の値になると乱流に遷移する。

 

①

（ア）プラントル数　（イ）ヌセルト数

（ウ）　レイノルズ数　（エ）レイリー数

 

②

（ア）ヌセルト数　　（イ）プラントル数

（ウ）レイリー数　　（エ）レイノルズ数

 

③

（ア）プラントル数　（イ）ペクレ数　

（ウ）レイノルズ数　（エ）ヌセルト数

 

④

（ア）プラントル数　（イ）ヌセルト数　

（ウ）レイリー数　　（エ）レイノルズ数

 

⑤　

（ア）ヌセルト数　　（イ）ペクレ数　　　

（ウ）プラントル数　（エ）レイリー数

 

解答

①

 

解説

［解くために必要な知識］

熱流体に関する無次元数

 

◆レイノルズ数Re

　強制対流における速度と粘性を用いて流れの特性を表す。

 

　Re=ux/ν

　

　ｕ：主流速度

　ｘ：前縁からの距離

　ν：動粘性係数　μ/ρ

　μ：粘性係数

　ρ：密度

◆グラスホフ数Gr

　自然対流の状態を表す。

 

　Gr=L³gβΔT/ν²

 

　Ｌ：代表長さ

　ｇ：重力加速度

　β：体膨張係数

ΔＴ：伝熱面と流体の温度差

　ν：動粘性係数　

 

◆ヌセルト数Nu

　熱伝達の強さを表す。

 

　Nu=hL/λ

 

　ｈ：熱伝達率

　Ｌ：代表長さ

　λ：熱伝導率

 

◆プラントル数Pr

　流れと熱移動の関係を表す。

　

　Pr=ν/a

ただしaは熱拡散率であり定圧比熱c_pと熱伝導率λ、密度ρを用いて次のように表されます。

　a=λ/(c_p・ρ)

 

　Pr=c_pρν/λ=c_pμ/λ

 

◆レイリー数Ra

　自然対流の状態を表す。

 

　Ra=Gr・Pr

 

　Ra＞5×10⁸　⇒遷移領域

　Ra>10¹⁰　　⇒完全に乱流

 

補足1　

平板上を流れる強制対流における前縁距離xについて図28.1をご覧ください。

 

補足２

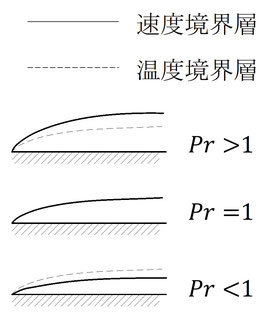
速度境界層と温度境界層の関係性を表すプラントル数について図28.2をご覧ください。

 

＊以上の無次元数の定義は覚えておきましょう

 

 

では問題を解いていきます。

 

図28.2に示すように温度境界層厚さと速度境界層厚さの比はプラントル数に依存します。［ア］

 

熱伝達率の無次元数はヌセルト数(Nu=hL/λ)になります。[イ]

強制対流の場合は一般にプラントル数とレイノルズ数の関数で表されます。[ウ]

 

自然対流においてはレイリー数が5×10⁸～10⁹程度から乱流に遷移し始めて10¹⁰に至ると完全に乱流になります。[エ]　　　//

 

 

 

＜前の問題へ　 次の問題へ＞

 

技術士試験対策Topへ戻る

 

 

令和3年解答解説へ戻る