図に示すように、質量mの機械がばね定数kのばねを介して床に固定されている。この機械に角周波数ωの正弦波状の力fが作用し、定常状態となったときに、床に伝達される周期的な力Fの振幅をfの振幅の50%未満にしたい。ばね定数の条件として、適切なものはどれか。

 

 

 

解答

①

 

[解くために必要な知識]

 

図21.1に示すようにmkcからなる系に周期的な強制力Fsinωtを作用させます。

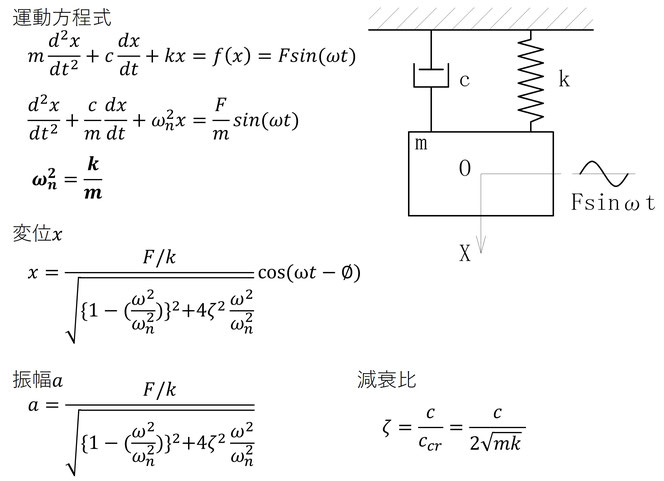
このとき、

 

運動方程式

　md²x/dt²+cdx/dt+kx=f(x)=Fsinωt

　d²x/dt²+c/mdx/dt+ω_n²x=f(x)=F/msinωt

　ただし、ω_n²=k/m

 

途中の計算はとばしますが、変位xと振幅aは図の通りです。

 

ダンパが無い場合、減衰比ζはゼロとなり、振幅は次の通りになります。

 

　a=F/k{(1-ω2/ω_n²)}

 

＊振幅aの式は、ダンパが無い場合は覚えておきましょう。できればダンパがある場合も覚えておきましょう。

 

では問題を解いていきます。

 

質量mとばねkから構成される系に外部強制力fsinωtが作用しています。

この系における振幅は次の通りです。

 

　a=f/{k(1-ω2/ω_n²)}=fω_n²/{k(ω_n²-ω²)}

　a=fk/{mk(k/m-ω²)}=f/{m(k/m-ω²)}

 

　a=f/(k-mω²)

 

これが質点mの振幅、つまり最大変位です。変位がaに達したとき、ばねはaだけ縮んでいる（あるいは伸びている）ことになります。つまりこのときばねの力をF_sとすると、F_s=kaとなります。

 

床面からはこのばね力に反発する力Fが発生します。

つまり

　F=-ka

となります。

これが機械に作用する力fの50%未満、F＜1/2fとなる条件を求めます。

 

　F=-ka<1/2f

　a=f/(k-mω²)

よって、

　-kf/(k-mω²)<1/2f

　-2k<k-mω²

　-3k<-mω²

 

　 k<1/3・mω²　　　　　//

＜前の問題へ　 次の問題へ＞

 

技術士試験対策Topへ戻る

 

 

令和3年解答解説へ戻る