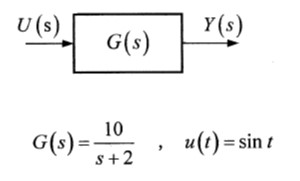
図のように伝達関数G(s)に入力u(t)を加えたときの定常出力y(t)として、適切なものはどれか。

 

 

解答

④

 

解説

［解くために必要な知識］

平成23年度に全く同じ問題が出ています。（Ⅳ-21）

 

【ラプラス変換】

代表的なラプラス変換表を図11.1に示します。

＊ラプラス変換表は問題で与えられる場合も多いのですが、本問のように与えられないこともあります。余力があれば一通り覚えましょう。

 

 

 

では問題を解いていきます。

 

入力信号u(t)=sint　をラプラス変換します。

 

　U(s)=L[sint]=1/(s²+1)

 

伝達関数G(s)とU(s)から出力関数Y(s)を求めます。

　Y(s)=G(s)×U(s)=10/(s+2)×1/(s²+1)

　Y(s)=2/(s+2) + (-2s+4)/(s²+1)

 

＊この展開は部分分数分解です。

　10/(s+2)×1/(s²+1)=A/(s+2)+(Bs+C)/(s²+1)

と置きます。右辺を通分して整理すると次式を得ます。

　(A+B)s²+(2B+C)s+A+2C=10

よって

　A+B=0

　2B+C=0

　A+2C=10

この3式から次を得ます。

　A=2

　B=-2

　C=4

よって、

　10/(s+2)×1/(s²+1)=(-2s+4)/(s²+1)

となります。

 

 

これを逆変換します。

　y(t)=2L^-1[1/(s+2)] - 2L^-1[s/(s²+1)] + 4L^-1[1/(s²+1)]

　y(t)=2e^-2t - 2cost + 4sint

 

定常時、つまりt→∞において、上式の第一項2e^-2tはゼロになります。

よって、

　y(t)=-2cost + 4sint

三角関数の合成より、

　y(t)=√(2²+4²)sint(t+α)=√20×sin(t+α)

　tanα=-2/4=-1/2 、　α=tan^-1(-1/2)　　//

 

 

＜前の問題へ　 次の問題へ＞

 

技術士試験対策Topへ戻る

 

 

令和3年解答解説へ戻る