Ⅲ-1

A群の用語とB群を組合わせたとき、A群の用語の中で対応する適切な用語がB群にないものはどれか。

 

A群

①ミーゼスの条件　②断面係数　③応力拡大係数

④フックの法則　⑤せん断応力

 

B群

降伏、共役、ヤング率、不静定、相当応力、破壊じん性、真応力

 

 

解答

②

 

解説

［解くために必要な知識］

（１）図1.1に示すように、材料を1方向に引張力（あるいは圧縮力）を与えた場合に生じるひずみε（イプシロン）を横軸に、生じる応力σを縦軸に取ります。これを応力－ひずみ曲線と言います。

 

応力とひずみはある点までは比例関係ですが、ある点で極大値を取り応力が減少します。さらに引っ張り続けると今度は極小値を取り応力は上昇し始めます。この極大値をとる点を上降伏点と言い、極小値をとる点を下降伏点と言います。

 

比例関係にある間は応力とひずみには縦弾性係数（ヤング率）Eを用いて次の関係がありますこれをフックの法則と言います。

　σ=Eε

 

 

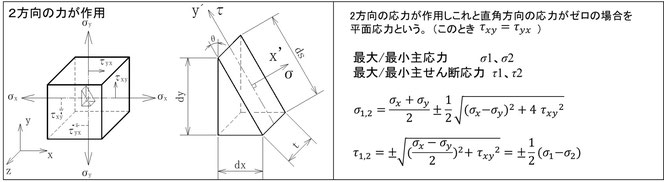
（２）図1.2に示すようにx,yの2方向に力が作用したときの、y軸を法線とする面に対しx方向のせん断力をτ_xyとする。このときx軸を法線とする面に対しy方向のせん断力τ_yxも必ず発生し両者の間には次の関係があります。これを共役せん断応力と言います。

 

　τ_xy=τ_yx

 

また、x,y,z3方向に応力が発生している状態では、材料のせん断ひずみエネルギーが一定の値に達すると降伏する条件をミーゼスの降伏条件と言い次の関係があります。

 

　𝜎_𝑉𝑀=√[1/2{(𝜎_x−𝜎_y)²+(𝜎_y−𝜎_z)²+(𝜎_z−𝜎_x)²}+6(τ_xy²+τ_yz²+τ_zx²]

あるいは最大主応力σ1、中間主応力σ2、最小主応力σ3を用いて、

　𝜎_𝑉𝑀=√1/2{(𝜎₁−𝜎₂)²+(𝜎₂−𝜎₃)²+(𝜎₃−𝜎₁)²}

 

𝜎_𝑉𝑀はミーゼス応力、あるいは相当応力と呼ばれます。

 

 

（３）応力拡大係数とは、材料が長さ2c、高さ2bの亀裂を有する場合、次式で定義されます。

　K=ασ√πc

ここでαは材料の形状や大きさ、亀裂の形状、応力の形式によって決まる無次元量数になります。

 

ところで材料力学においては破壊の基準は基準応力σ_Bを用いて次式で表されます。

　σ≧σ_B

亀裂を有する材料に荷重がかかったとき、理論上は亀裂の先端で無限の応力が発生します。これでは少しでも荷重がかかったときに必ず破壊に至るになります。しかし実際にはそうはなりません。亀裂を有する場合は応力基準での強度評価ではなく、破壊力学にのっとった破壊基準での評価が必要になります。それが次の関係式です。

　K≧Kc

Kcは亀裂が進展を開始する際の応力拡大係数の値で、破壊じん性値と呼ばれます。

 

（４）一様断面で長さLをもつ材料をはり、あるいはビームと呼びます。この材料を何らかの方法で支持し荷重を加えたとき、例えば□19mmの角棒の片端を固定し他端に集中荷重を作用させた場合、生じる応力は次式の通り。

　σ=M/z

このzは材料の断面の形状で決定される値で断面係数と呼ばれます。

 

（５）未知の反力数が4つ以上ある状態を不静定と言います。力の釣り合いだけでは反力が計算できないはりを不静定はりと言います。

代表的な不静定はりとして両端固定はりがあります。

 

（６）断面積Aの材料に引張力Pを与えたときの応力σは次式で表されます。

　σ=P/A

このσは正確には公称応力と言います。

引張力Pを与えられたとき、正確には断面積にも変化が生じます。この断面積の変化を考慮した応力を真応力と言います。真応力をσ'とし、このときの断面積をA‘、とすると

　σ‘=P/A’

となります。

 

＊以上、言葉の定義は覚えておきましょう。

 

では問題を解いていきます。

 

A群の用語に対応するB群の用語

①ミーゼスの条件　⇒　相当応力

②断面係数　　　　⇒　該当なし　　

③応力拡大係数　　⇒　破壊じん性

④フックの法則　　⇒　降伏、ヤング率

 

⑤せん断応力　　　⇒　共役　　//

次の問題へ＞

 

技術士試験対策Topへ戻る

 

 

令和3年解答解説へ戻る