図に示すように、片持ち梁に等分布荷重wを作用させている。自由端におけるたわみとして、最も適切なものはどれか。ただし、はりの曲げ剛性をEIとする。

◆両端支持梁

　◆等分布荷重wを受ける。

　　・反力　　　R1=R2=wL/2

・せん断力　F=w(L-2x)/2

（x=0もしくはLで最大値、wL/2、-wl/2をとる。）

・曲げモーメント　M=wx(L-x)/2　（x=1/2で最大値、wL²/8となる。）

・たわみ　y=5wL⁴/384EI　（x=1/2で最大たわみをとる。）

　◆自由端に集中荷重Pを受ける。

　　・反力　　　R₁=PL₂/L　、　R₂=PL₁/L

・せん断力

　F₁=-PL₂/L　（0≦x≦L₁）

　F₂=-PL₁/L　（L₁≦x≦L）

・曲げモーメント

　M=PxL₂/L　（0≦x≦L₁）

　　M=PxL₁/L　（L₁≦x≦L）

　　Mmax=WL₁L₂/L（x=L₁）

また、L₁=L₂=1/2Lのとき、

　　Mmax=PL/4　となる。

・たわみ　＊L₁=L₂=1/2Lのとき梁の中心1/2Lで生じる最大たわみ

　y=wL³/48EI

＊以上は全てを覚えることが理想ですが、いきなりすべて覚えるのは難しいと思います。繰り返し過去問を解く中で少しづつ覚えていくのがいいと思います。

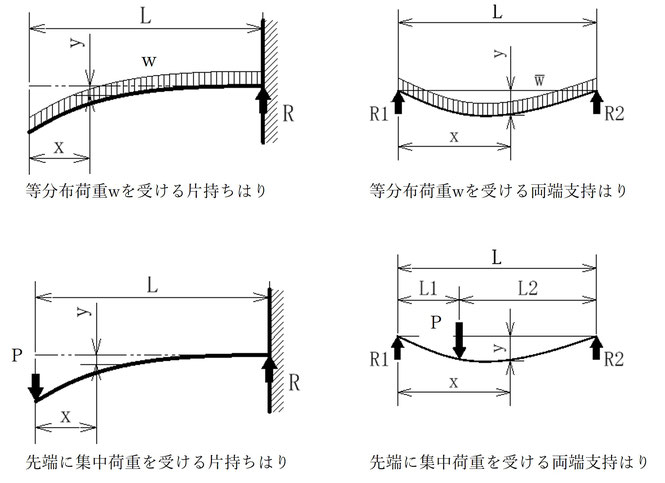
問題は等分布荷重をうける片持ち梁ですので、自由端におけるたわみは次の通りです。

y=wL⁴/8EI　//

［別解］

たわみ基本式

d²y/dx²=-M/EI

曲げモーメントM

M=-wx²/2

たわみ基本式に代入。

d²y/dx²=wx²/2EI

積分する。

dy/dx=1/EI(wx³/6+C)

＊Cは積分定数

x=L（固定端）において、dy/dx=0（たわみ角ゼロ）

よって　C=-wL³/6

dy/dx=w/6EI(x³-L³)

積分する。

y=w/EI(1/24x⁴-1/6L³x+C₁)

＊C₁は積分定数

x=L（固定端）においてy=0（たわみゼロ）

C₁=wL⁴/8

y=w(x⁴-4L³x+3L⁴)/24EI

x=0において、

y=wL⁴/8EI　//

<前の問題へ　次の問題へ>

技術士一次試験対策Topへ戻る

技術士一次試験対策　令和2年へ戻る