外力によって生じる振動に関する次の記述の、［　　　］に入る語句の組合せとして、最も適切なものはどれか。

　系が外部から加振されて調和振動するとき、加振力の振幅が一定でもその振動数により、振動の振幅が変化し、ある振動数で振幅が［　ア　］になる。この現象を［　イ　］という。この現象が生じる振動数を［　ウ　］という。［　イ　］では、加振の開始とともに発生した振動が時間とともに増大し、その振幅は、不減衰系では［　エ　］になる。

①　ア：極大　イ：共振　ウ：固有振動数　エ：有限な値

②　ア：極大　イ：共振　ウ：共振振動数　エ：無限大

③　ア：極大　イ：強制振動　ウ：共振振動数　エ：無限大

④　ア：零　イ：共振　ウ：励振振動数　エ：無限大

⑤　ア：零　イ：強制振動　ウ：固有振動数　エ：有限な値

解答

②

解説

図19.1に示す用に質量m、ばね定数kのばね、減衰係数cのダンパからなる系に外部からの強制力Fsinωtを与えます。このときの変位xは図に示す通りです。

ただし、ζは減衰比でζ=c/2√(mk)、ω_nは固有角振動数でω_n=√(k/m)です。

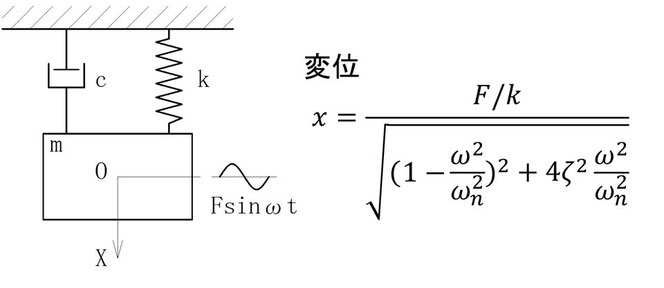
問題にある、加振力の振幅が一定とはFが一定という事です。また振動数ωが変化すると振動の振幅つまり変位ｘは変化します。

この変位xはある振動数で極大になります（ア）。この現象を共振といいます（イ）。この現象が生じる振動数を共振振動数といいます（ウ）。

減衰が無い場合、ζ=0となるので、その変位は次の通りです。

x=(F/k)/√[(1-ω²/ω_n²)²]

ω=ω_nのとき分母がゼロになるためxは無限大となります（エ）。　　//

<前の問題へ　次の問題へ>

技術士一次試験対策Topへ戻る

技術士一次試験対策　令和2年へ戻る