内径d=120[mm]、厚さt=2[mm]の薄肉の円筒状圧力容器がある。この容器に一様な内圧を加え、端部から離れた円筒部中央の外壁における円筒軸方向のひずみを測定したところ、32×10^-6であった。加えた内圧として、最も近い値はどれか。ただし、材料の縦弾性係数E= 206[GPa]、ポアソン比ν=0.3とする。

 

①2.20 MPa

②1.10 MPa

③0.55 MPa

④0.26 MPa

⑤0.13 MPa

 

解答

②

 

解説

［解くために必要な知識と周辺知識］

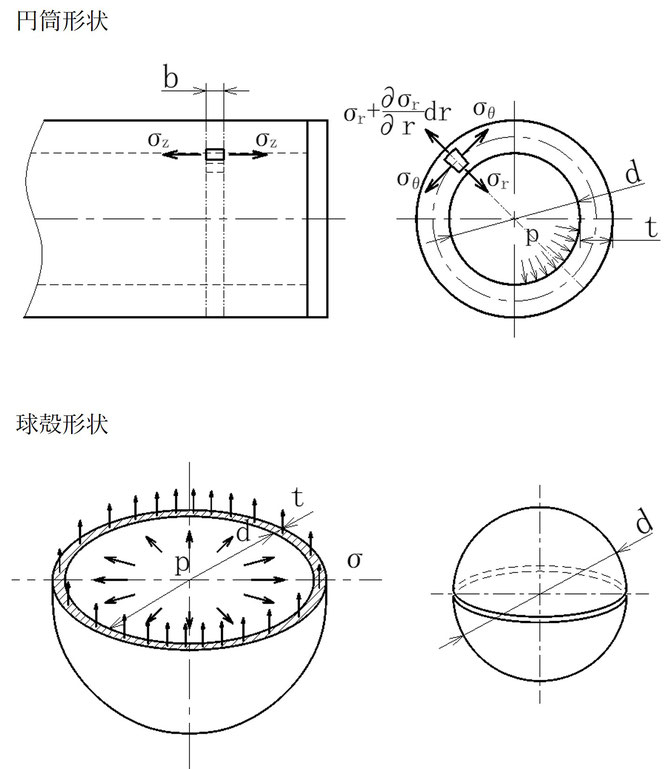
◆内圧Pが作用する肉厚t、内径dの円筒形状に発生する応力

・軸方向応力

　σ_z=Pd/4t

・軸方向ひずみ

　ε_z=(σ_z-νσ_θ)/E

・円周方向応力

　σ_θ=Pd/2t

・円周方向ひずみ

　ε_θ=(σ_θ-νσ_z)/E

ただし、νはポアソン比

 

◆内圧Pが作用する肉厚t、内径dの球殻形状に発生する応力

・σ=Pd/4t

 

＊それぞれの関係式は覚えておきましょう。

 

では解いていきます。

題意から、ε_z=32×10^-6

 

ε_z=(σ_z-νσ_θ)/E=(Pd/4t-νPd/2t)/E

ε_z=P(d/4t-νd/2t)/E

P=Eε_z/(d/4t-νd/2t)=4tEε_z/(d-2dν)

問題文の数値を代入してPを求めます。

 

P=4×2×206×10⁹×32×10^-6/(120-2×120×0.3)=1,098,7 00[Pa]　//

<前の問題へ　次の問題へ>

 

技術士一次試験対策Topへ戻る

 

技術士一次試験対策　令和2年へ戻る