技術士一次試験 · 09日 1月 2022

技術士一次試験　専門科目　機械部門　R1　Ⅲ-21

令和1年

図のように、長さlの一様な細い棒が、一端を軸として摩擦なしに回転できるようになっている。この棒を水平にして静止させ、次に静かに手を離して回転させる。このとき、鉛直になった瞬間における棒の角速度として、最も適切なものはどれか。ただしgは重力加速度とする。

解答

③

解説

［解くために必要な知識と周辺知識］

回転する物体の運動エネルギーは1/2・Iω²です

位置エネルギーはmghです。

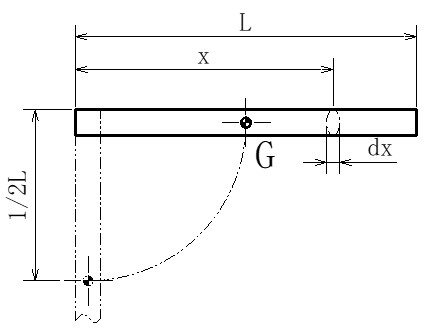
図21.1に示すように、長さLの棒が水平方向から左端を軸として時計回りに鉛直下向きまで回転したとき、高さhは重心Gの変位量で1/2Lとなります。

この棒の慣性モーメントを求めていきます。

I=∫r²dm

I=∫x²dm=∫x²m/L・dx=m/L・1/3x³（積分範囲は0からLまで）

I=1/3mL²

つまり、長さLの棒の慣性モーメントは1/3mL²となります。

＊回転体の運動エネルギーと棒の慣性モーメントは覚えておきましょう。

では問題を解いていきます。

エネルギー保存則から、位置エネルギー=運動（回転）エネルギー

　mgh=1/2・Iω²

h=1/2L、I=1/3mL²を代入します。

　mg(1/2L)=1/2・1/3mL²ω²

　ω²=(mgL)/(1/3mL²)=3g/L

　ω=√(3g/L)　　//

コメント: 0