今回は令和一年再試験Ⅲ-34
技術士一次試験の機械部門過去問の中でも直近3年間、2017年から2019年の中で、え?これ難しくね?って思った問題をピックアップして解説します。2019年は再試験があるので4回分の過去問からのピックアップです。
解説して欲しい問題があったらご連絡ください。
それでは問題です。
令和一年再試験、流体工学からの問題です。
Ⅲ-34 無限に広い空間内で、平板がその面内方向にU=U∞cos(ωt)の速度で振動している。このとき、流体の運動は∞平板の振動方向に平行であり、速度分布U(t,y)は、以下のように表される。
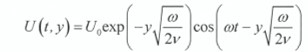
ここで、t,y,U0ω,νは、それぞれ時間、流体と接する壁面を原点とする壁面垂直方向座標、振動の振幅、各振動数、流体の動粘性係数を表す。
下図は上式の概念を表しており、y方向に振動振幅が減衰していく様子を示している。ここで、流体の速度変動の振幅がU0の1%以上となる領域を境界層と定義する。流体を空気(ν=1.5×10^-15m^2/s)、振動数を1.0Hz(ω=2πrad/s)とするとき、境界層厚さδの値として、最も近い値はどれか。ただし、必要に応じて、log10=2.30(logは自然対数を表す)を用いよ。
①0.10㎜
②0.40㎜
③10㎜
④100㎜
問題文、以上

問題に対するコメント
これ、難しくないですか?難しいですよね。何が難しいって流体のカテゴリーで出題されているにもかかわらず実は流体の知識は必要ないんですよね。じゃあ振動の知識が必要かというとそうでもない。解き方をひらめくかどうかがポイントなんですよね。
もし私が受験生だとしてこの問題があったとしたらパスしますね。他の問題に取り組みます。私の記事では基本的にそういったひらめきを要する問題を難問と定義して難問の解説を行います。
解答のポイント
U(t,y)/U0=0.01(1%)だ!
「流体の速度変動の振幅がU0の1%以上となる領域を境界層と定義する。」この記述から上の関係であることが分かります。
式で表すと次の通りです。

ここでU(t,y)はcos(***)が1となるときに最大値を取ります。よってcos(***)=1とおきます。
すると上式は次の通りになります。

ここでlogの性質を振り返ります。

よって先の式は次のように変換されます。
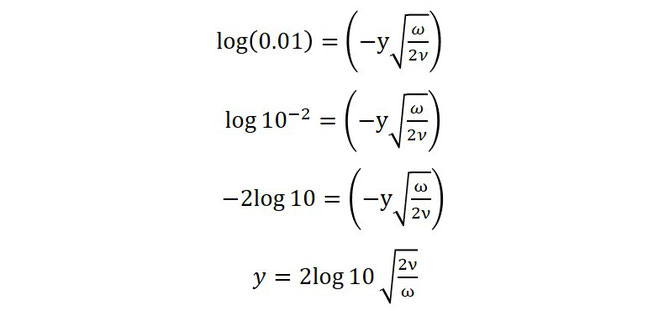
ここまで来たら後は数値を代入するだけです。

ポイントに気づくことができればあとは簡単です。気づくことができなければ非常に厄介な問題です。難しいポイントとしては①流体工学のカテゴリーで出ている。②振動の知識で解けるかと思ったらそうでもない。③複雑そうに見せていて実は簡単。(ポイントに気づけば瞬殺)
1次試験はあくまで基礎知識を問う試験です。複雑そうに見えても実は簡単という問題も多いです。ここが落とし穴でして、技術士試験!難しい!と思ってしまうと簡単な問題も難しく見えてしまいます。
何でもない柳の木が幽霊に見えてしまうのと同じ心理ですね。
前のブログはおススメ技術サイト一覧です。
次のブログは同じく制御の難問です。
コメントをお書きください