設計知識 · 11日 2月 2021

技術士1次試験に出てくるラプラス変換

はじめに

技術士機械部門の一次試験は基本的に4力、すなわち材料力学・機械力学・熱力学・流体力学、の知識が問われます。

ここで直近5年程度の過去問から4力の中でも特に機械力学に着目すると、その中でさらに制御工学が明確に区分できるように思います。

制御工学に区分できる問題の代表例としては、

・ブロック線図から伝達関数を求める問題。

　・伝達関数から極あるいは零点を求める問題。

　・像関数F(s)が与えられていて逆ラプラス変換を求める問題。

　・系の安定性を求める問題。

などがあります。「機械力学」に分類できる問題は毎年12問程度の出題がありますが、その中の4問程度は制御工学に分類できる問題となっています。

　「伝達関数」や「ラプラス変換」は制御工学を扱う上で非常に重要なキーワードですが、それを単体で扱っていては、つまり伝達関数の求め方やラプラス変換の計算を問うだけでは、機械力学という分野の中でそれがどのように応用されていくのかがわかり難いように思います。

　知識を問う問題としてはいいのですが、私はどんな知識でも「その知識がどのように応用されるのか」が見えないとなかなか覚えられません。そこでラプラス変換や伝達関数がどのように応用されるのかの基本を見ていきたいと思います。

　結論としては

（１）ある系に対して運動方程式をたてる。

（２）運動方程式をラプラス変換する。

（３）伝達関数を求める。

という手順で応用されます。具体的に見ていきます。

図１に示すような質量mの物体がばね定数kのばねと減衰係数cのダンパで支持されています。この質量mに外部から強制力W (t)を与えたときの変位量をx(t)とします。

このときの運動方程式は次の通りです。

・・・①式

ここである関数f(t)をn階微分したものをラプラス変換すると次のようになります。

前出の変位量x(t)について考えます。t=0でx(0)=0、x’(0)=0となります。

よって

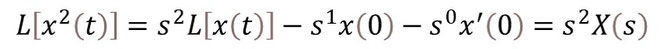
また、

以上から①をラプラス変換すると

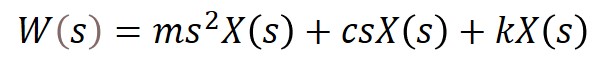
・・・②式

まずは②式を変形します。

　ところで、ある系へのインプット(In)と系からのアウトプット(Out)との関係は伝達関数Gを用いて次のように表されます。

　Out=G・In

　G=Out/In

　いま、問題の系には入力として外力W (t)、出力として変位x(t)があります。よって伝達関数Gは次の通りです

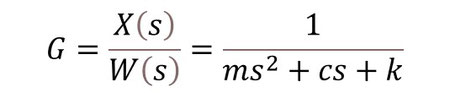
これをブロック線図で表すと、入力F(s)、伝達関数G、出力X(s)であり図の通りです。

　以上のように運動方程式をラプラス変換することで系の伝達関数を求めることができます。

時間関数（t関数）からなる微分方程式を解くのはとても難しいので、この方程式にラプラス変換という数学的操作を加えて別の関数（s関数）に変換し、s関数相互間の問題として扱うと計算がとても楽になります。

前のブログは電気自動車とガソリン自動車のCO2排出比較です。

<前のブログへ　次のブログへ>

コメント: 0