今回は平成29年Ⅲ-12
技術士一次試験の機械部門過去問の中でも直近3年間、2017年から2019年の中で、え?これ難しくね?って思った問題をピックアップして解説します。2019年は再試験があるので4回分の過去問からのピックアップです。
解説して欲しい問題があったらご連絡ください。
それでは問題です。
平成29年、制御工学からの難問です。
Ⅲ-12 下図に示すフィードバック制御系が安定に動作するためのゲインKの範囲として最も適切なものはどれか。
①0<K<1.2
②0<K<2
③0<K<6
④0<K<15
⑤0<K30

これは知っていれば解けるタイプの問題ではあります。が、難しい。要求される知識ポイントが3つ。
(1)伝達関数の導出
(2)特性方程式からの判別
(3)高次方程式の安定判別法
よくある問題のパターンとしては、もう少し複雑なブロック線図が与えられて伝達関数を導出するもの。
あるいは伝達関数が与えられて安定判別を行うもの。それも分母=ゼロとしたときの解=極を求めて、実数部が全てマイナスであれば安定という条件のもと安定判別を行うもの。
この2パターンですが、この問題はこの2パターンが盛り込まれているうえに、極を求めることが出ないため安定判別法による判定が必要になります。
判別法はフルビッツの安定判別法かラウスの判別法。どちらでも判定は可能です。
(1)伝達関数を導出し特性方程式を導きます。
ブロック線図の描き方と等価交換は図2の通りです。

問題文はフィードバック結合です。またフィードバック信号=G1となります。よってこの系における伝達関数は次の通りです。

この伝達関数の分母をゼロとおいて特性方程式とします。
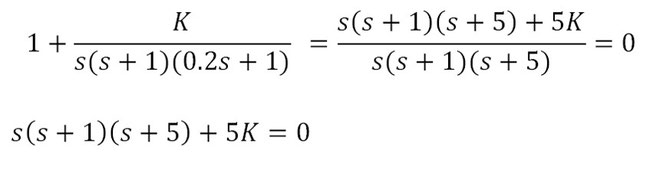
(2)-1フルビッツの判定法
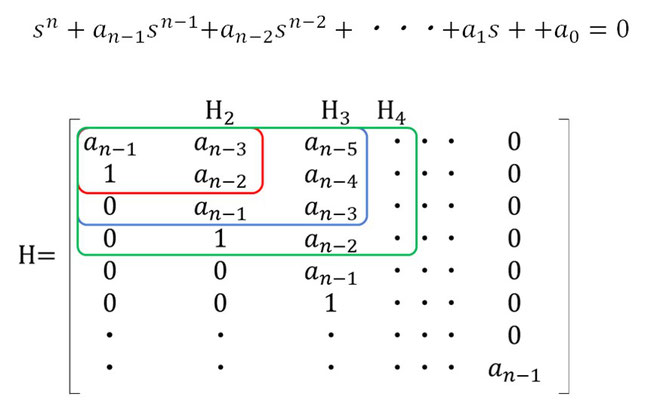
特性方程式が次の式で与えられたときに行列Hを作る。
このとき次の条件を満たせば系は安定する。
①特性方程式の係数𝒂_𝒊(𝒊=𝟎 , 𝟏 , 𝟐 , 𝟑 , ・・・ , 𝐧−𝟏)が全て正であること。
②行列式𝑯_𝒊 (𝒊=𝟑 , 𝟒 , 𝟓 , ・・・ , 𝐧−𝟏)が全て正であること
ではこの条件を確認していきます。
(2)-2フルビッツの判定法の適応
問題文から導出した特性方程式を展開します。

全ての係数が全て正という条件から5K>0➡K>0という条件がまず求まります。
次に、行列式を作成します。
次数が3のためH3とH2の二つの行列式ができます。
まずはH3を作成します。(図7の青枠参照)

3×3の行列式は次の図の通りに計算でき、安定のためにはその値が正である必要があります。

行列式H2を作成します。
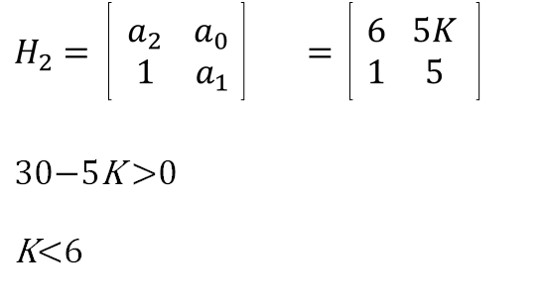
よって安定の条件として
K>0、
K<6
となり解答は③になります。
(3)-1ラウスの判定法
ラウス整列を求めます。その手順は図10にある通りです。

このとき次の条件を満たせば系は安定する。
①特性方程式の係数𝒂_𝒊(𝒊=𝟎 , 𝟏 , 𝟐 , 𝟑 , ・・・ , 𝐧−𝟏)が全て正であること。
②ラウス整列𝑹_𝒊𝟏(𝒊=𝟑 , 𝟒 , 𝟓 , ・・・ , 𝐧−𝟏)が全て正であること。
ではこの条件を確認していきます。
(3)-2 ラウスの判定法の適応
特性方程式からラウスの係数を求めていきます。


本問題における各ラウスの係数は次の通り。

全ての係数が正である必要があるため、次の関係が成り立つ。

安定判定法を知っていれば解ける問題ではありますが、複雑です。正直私が受験生だったとするとこの問題はパスします。
複雑ゆえに時間がかかり、かつ単純ミスによる誤答の可能性が出やすいからです。
他の問題が終わってよっぽど時間があまれば別ですが、おおよそ1問にかけられる時間の目安は5分。複雑すぎる問題は避けたほうがベターでしょう。
前のブログは流体の難問です。
次のブログは熱工学の問題です。
コメントをお書きください