◆工程能力指数で工場の実力を数値化しよう!
◆工程能力指数の計算式
設計者A「図面指示では公差が±0.1だけど、切削加工だし実力としては100分台で出るよね。」
加工者B「まぁそれくらいは大丈夫ですよ。」
*100分台で出る=±0.01程度の精度でできる。
よくある会話です。この会話に出てくる「実力」を測る指標が工程能力指数です。
工程能力指数にはCpとCpkの2つがあります。まずは式を確認しましょう。

Cpの計算前提として2つの条件があります。
①すべてのデータが上下限規格値内にある。
②データの平均値が規格範囲の中心値である。
実際の製造工程ではこの2条件はあり得ません。必ずデータの平均値と規格値にはズレが生じます。このズレを考慮した指標がCpkになります。
Cpkは上限規格、下限規格でそれぞれ計算し小さい方の値をとります。
*標準偏差の計算についてはこちら⇒[正規分布と標準偏差]
◆工程能力指数を具体的に計算しよう。
具体的な計算例を見ていきましょう。
図1に示すように寸法aの指示が6.0+0.3~-0.2だった場合、上下限規格値は次のようになります。
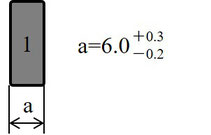
上限規格値 6.3
下限規格値 5.8
ある工場で1ロット分生産し20個を抜き取り検査した結果が表1の通りだった場合、工程能力指数Cpkは次の通りになります。
*データ群から標準偏差σを算出するにはこちら:
標準偏差σの計算 [正規分布と標準偏差]

工程能力指数の計算
平均値 A=5.894
標準偏差 σ=0.039
この正規分布を書くと、下図になります。
規格中央値6.05に対し、平均値が5.894と低くなっているため上限規格値を上回ってしまう可能性に比べて下限規格値を下回ってしまう可能性は高くなります。

表1 加工寸法抜き取り検査データ
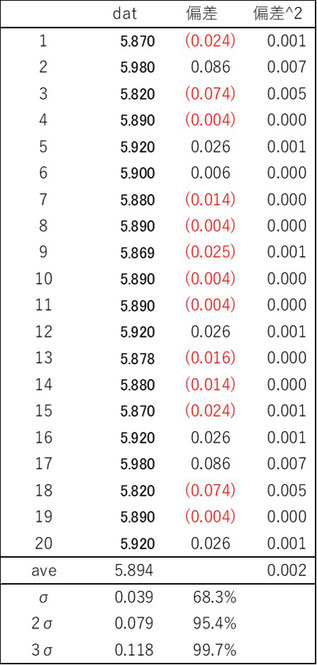
◆工程能力指数の意味を確認します。
工程能力Cpkの値と、不良発生率の関係性は下表の通りです。
片側規格というのは、上限もしくは下限どちらか一方という意味です。
Cpk(下限)=0.79
ということは、0.66~1.00の間でありつまり不良が発生する確率としては
下の表から2.3%~0.14%の間にあります。
仮に1ロット1,000個作って20個抜き取り検査の結果がCpk(下限)=0.79であったとすると
1~2個程度(0.14%)~最大で25個程度(2.3%)、3σから2σ程度の下限不良品が1ロット1,000個の中に含まれている可能性があります。
取得した品質データを工程能力指数Cpkで整理すると、工場の実力が見えてきます。

◆CpとCpk
上記はあくまで片側規格値です。ここで仮に次のような結果を想定します。
Cpk(上限)=0.33
このときCp=1.00だったとするとCpk(下限)が計算できます。
この計算は後述しますが、この場合は
Cpk(下限)=1.67になります。
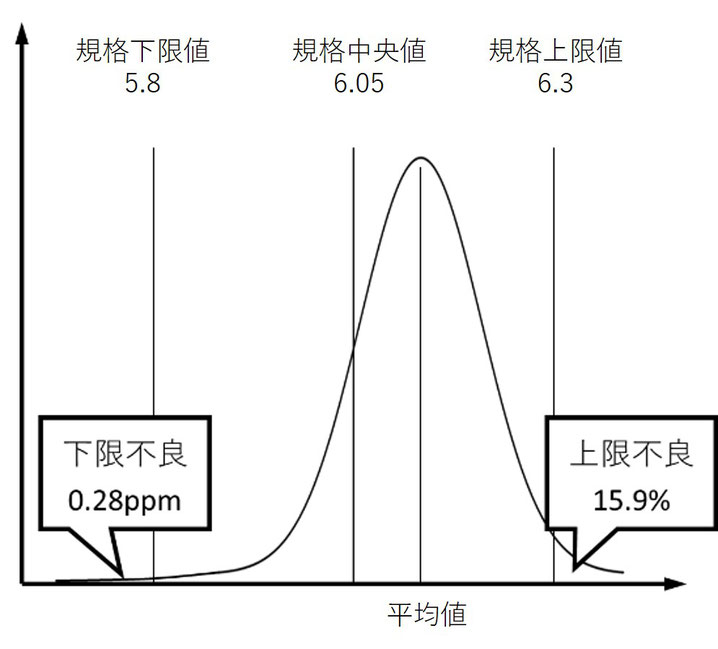
この正規分布は図(a)のような形になります。
上限不良は15.9%、下限不良は0.28ppmの発生確率になります。
この状態で、「バラつきをそのままに平均値を規格中央値に近づけるように設備パラメータを調整する」ことができれば図(b)のような状態を作り出すことができます。
Cp=1.00
Cpk(上限)=1.00
Cpk(下限)=1.00
バラつきはそのままに平均値を調整する方法はこちらの記事を確認してください。
Cpk(上限)=0.33では不良率は15.9%+0.28ppmになりますが、
上手く調整してCpk(上限)≒Cpk(下限)≒Cp≒1.00に近づけることができれば不良率は0.14%(上限)+0.14%(下限)=0.28%まで改善されます。

◆補足CpとCpk(上限)Cpk(下限)との関係性
Cp=(上限規格値-下限規格値)/6σ
Cpk(上限)=(上限規格値―平均値)/3σ
Cpk(下限)=(平均値ー下限規格値)/3σ
Cpk(上限)とCpk(下限)を足します。
Cpk(上限+下限)=[(上限規格値―平均値)+(平均値ー下限規格値)]/3σ
Cpk(上限+下限)=(上限規格値ー下限規格値)/3σ
Cpk(上限+下限)=2Cp
前述の例では、
Cp=1.00
Cpk(上限)=0.33
Cpk(下限)=1.67
Cpk(上限+下限)=0.33+1.67=2×1.00
上記の関連ブログ[正規分布と標準偏差]から、20個のデータを入力すれば「標準偏差と工程能力指数を計算し、正規分布も自動で描く」エクセルシートがダウンロードできます。
前のブログは稼動率と可動率についてです。
次のブログは正規分布と標準偏差です。
コメントをお書きください