令和3年
Ⅲ-35
水平に設置された円管内に流体が流れており、流れ方向の位置AからBの区間において、断面積がSAからSBへと緩やかに減少している。2点A、B間の圧力差を水銀柱で測ったところ、水銀柱の高さはHであった。重力加速度をg、流体の密度をρF、水銀の密度をρMとし、水銀の密度は流体の密度に対して十分に大きいと仮定してよい。
位置Aにおける円管内断面積平均速度として、最も適切なものはどれか。ただし、粘性の影響は無視してよい。
解答
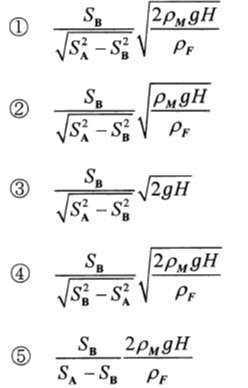
①
解説
[解くために必要な知識]
ある系に流入する流体とそこから流出する流体の間には次の関係が成り立ちます。
◆ベルヌーイの定理
ρV2/2+P+ρgz=一定
◆質量保存の法則
Q=AV=一定
ただし、
ρ:密度
V:流体速度
P:流体圧力
g:重力加速度
z:流体の高さ
Q:体積流量
A:流路断面積
V:流体速度
では問題を解いていきます。
A点における速度をVA、圧力をPA、高さをzAとして、B点におけるそれぞれをVB、PB、zBとします。
図35.1に示すように円管は水平に置かれているためzA=zBとなります。

ベルヌーイの定理から
ρFVA2/2+PA=ρFVB2/2+PB
VA2/2+PA/ρF=VB2/2+PB/ρF
質量保存の法則から
Q=SAVA=SBVB
VB=SAVA/SB
ベルヌーイの式に代入します。
VA2/2+PA/ρF=(SAVA/SB)2/2+PB/ρF
SA2VA2/(2SB2)-VA2/2=PA/ρF-PB/ρF
(SA2-SB2)VA2/2SB2=(PA-PB)/ρF (1)
また、圧力差と水銀の位置ヘッドρMghと流体の位置ヘッドρFghの関係は次の通りです。
PA-PB=gh(ρM-ρF)
問題文水銀の密度は流体の密度に対して十分に大きいと仮定してよい、とあるから
ρM-ρF≅ρM
とおける。
これを(1)式に代入します。
(SA2-SB2)VA2/2SB2=ghρM/ρF
(SA2-SB2)VA2=2SB2ghρM/ρF
VA2={SB2/(SA2-SB2)}・{2ghρM/ρF}
VA=SB/√(SA2-SB2)・√{2ghρM/ρF} //
コメントをお書きください
教えて下さい (火曜日, 19 4月 2022 05:54)
技術士会の回答と異なります。
どちらが正解なのでしょうか。
ご教示願います。
管理人 (火曜日, 19 4月 2022 09:18)
ご連絡ありがとうございます。
技術士会のHPにアップされている解答を改めて確認しました。
令和3年度 技術士第一次試験【Ⅲ専門科目】試験問題の正答
1.機械部門
問題番号Ⅲ-35の正答番号を確認すると「1」になっています。
いかがでしょうか。下記urlご確認ください。
https://www.engineer.or.jp/c_topics/004/attached/attach_4106_1.pdf
教えて下さい (水曜日, 20 4月 2022 04:39)
確認ありがとうございます。
解答のなかで、こちらの(ρM-ρF)と
試験問題の正答①の選択肢 ρM
で少し異なるようです。
その点についてご教示頂けたらと
思います。
教えて下さい (水曜日, 20 4月 2022 04:56)
すみません。
問題文に"水銀の密度は流体の密度に対して十分に大きいと仮定してよい。"とあり、そのためρF≒0として消えていることがわかりました。
ありがとうございました。
教えてください (水曜日, 20 4月 2022 07:32)
確認ありがとうございます。
問題文に"水銀の密度は流体の密度に対して十分に大きいと仮定してよい。"
とありますのでρFは0としてρM-ρF=ρMとなることが分かりました。
ありがとうございました。
管理人 (水曜日, 20 4月 2022 19:45)
ご指摘ありがとうございます。
そして、解答が不十分となってしまっており大変申し訳ありませんでした。仰る通りで問題文から、ρM-ρF≅ρMとおけます。
また何かお気づきのことがありましたらご指摘いただけると幸いです。
教えて下さい (木曜日, 21 4月 2022 04:39)
確認、対応ありがとうございました。