はじめに
表1
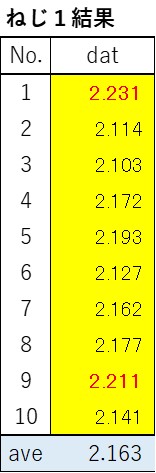
表2

表3

前回の記事でみた3本のねじ締め結果の表からわかることは何でしょうか?
表1から、ねじ1の締め付け結果は全体的に高い値であることがわかります。(平均値も高めの2.163となっている。)
表2から、ねじ2の締め付け結果は全て比較的、狙いの2.0に近い値になっています。
表3から、ねじ3の締め付け結果は全体的に低い値であることが分かります。
平均値と生データからこの程度のことは読み取れますが、これをぱっと見でわかるようにするために正規分布を描き、さらに工程能力指数を算出します。
[データ整理]
標準偏差、確率密度を計算したものを表4~6に、正規分布を描いたものを図1~3に示します。
また、上限値(Upper Limit Standard)2.2N/m、下限値(Lower Limit Standard)から工程能力指数Cp、Cpk(上限)、Cpk(下限)を算出します。
参考⇒「正規分布と標準偏差」こちらの記事から標準偏差と工程能力指数を計算し、正規分布を描くためのエクセルシートをダウンロードできます。
表1

表2

表3




まず工程能力指数を確認します。
ねじ1の上限および下限の工程能力指数を抜粋します。
「Cpk(上限):3.01」「Cpk(下限):0.31」
図4に示すように、
Cpk=0.33のとき15.9%の確率で規格外となります。よってCpk(上限)=0.31ということはこれ以上の確率で規格外=不良が発生することになります。
Cpk=2.00のとき0.001ppmの確率で規格外となります。よってCpk(下限)=3.01ということはもっと小さな確率となり不良が発生する可能性はほぼありません。
実際のデータを確認すると、10個のうち2個が上限不良となっています。(20%の不良)

図1~3に示す正規分布からは直接数値は読み取れませんが、上限下限不良のどちらが発生しやすい状態にあることが一目瞭然となっています。
ここで工程能力指数Cpを確認すると1.67となっています。これをどう読み取るか?ですが、「設備が理想の状態にあるときにはCpk(上限)=Cpk(下限)=Cpとなる」ことを意味します。「設備が理想の状態にある」とはここでは、その設備で製造した結果のデータの平均値が基準値に等しくなることを意味します。
ねじ締めの例では測定した増し締めトルクデータの平均値が設計値2.0N/mと等しくなるという事です。
設備のパラメータを上手く調整してあげて理想状態に近づけると上下限それぞれの工程能力指数が1.67程度になります。ちなみに1.67というと発生確率が0.28ppmです。上下限それぞれが0.28ppmとなるので、トータルとして0.56ppmの不良発生率になります。
*ppm(part per million):百万分の一
直行率の改善
工程能力指数Cp=1.67ということはこの設備はこの程度の実力を持っているという事です。ねじ1の場合はこれに対して、平均値が上限によっているため上限不良が発生する確率が高くなります。
自動でのねじ締めを考えたときに設定できる項目として「締付トルク」「ドライバー回転数」「ドライバー鉛直方向の押し付け力」「ねじの推進との同期速度」などが挙げられます。
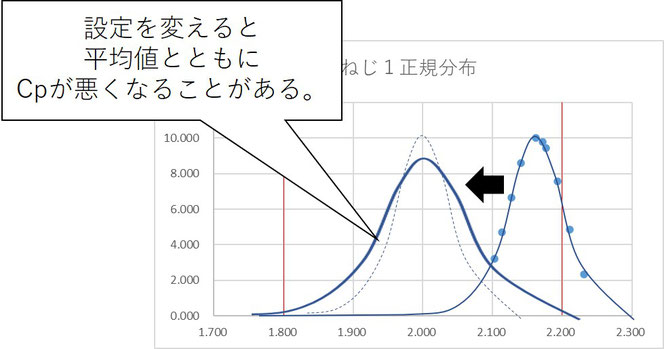
この中で平均値を下げるためにはまず締付トルクの設定値を下げます。このとき平均値が下がるとともに工程能力Cpが悪くなることがあります。(ばらつきが大きくなる。)
このときさらに改善するためには、他の設定項目も調整してばらつきを抑制する必要があります。ばらつきの評価に関してはこちらの記事をご確認ください。
前のブログは直行率と歩留まりについて
次のブログは生産技術系の人間が考えるDXです。
技術資料一覧はこちらから⇒「技術資料」
他のおすすめサイト一覧はこちらから→「おススメ!技術サイト一覧」
コメントをお書きください