◆A=tanθのとき、arctanA=θ
◆はじめに
機械設計をやっていると割と三角関数を使って計算します。その中で私が個人的に最もお世話になっている関数はアークタンジェント、タンジェントの逆関数です。本題に入る前に三角関数についておさらいしておきます。なお、この記事においての計算はエクセルを使用することを想定しています。最後にExcelでの計算式を一気に記載しています。
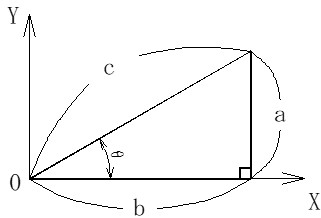
図1に示すような直角三角形の3辺、abcと角度θの間には次のような関係があります。
三角関数
sinθ=a/c
cosθ=b/c
tanθ=a/b(sinθ/cosθ)
逆三角関数
arcsin(a/c)=θ
arccos(b/c)=θ
arctan(a/b)=θ
◆XとYの位置から角度を計算
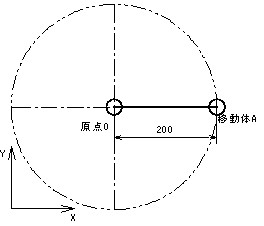
図2のように原点Oを中心に回転移動する移動体Aがあり、この移動体Aを図3のように原点からX方向150㎜(-50mm)まで移動させたい。角度ではなく距離が先にあるというのは割とよくあります。ではこのときの回転角度θはいくつでしょうか。ざっくりいくと40°です。もう少し正確に行くと41°です。もっと正確に行くと、41.4°、41.41°、41.40962・・・となります。

1.移動距離bから回転角度θの計算
計算過程を見ておきます。
b=150
c=200
a=(200^2-150^2)^(1/2)=132.29
*aを求める式は定理の中で最も有名なものの一つであるピタゴラスの定理、三平方の定理ともいう。
arctan(a/b)=arctan(132.29/150)=0.722734・・・[rad]
計算結果の角度はラジアン(弧度法)になります。°(度数法)への変換には次式を用います。
[ラジアン×180/π]
角度=0.722734×180/π=41.40962・・・
ここまでは単なる三角関数のお話し。では機械設計におけるどのような場面で使うのか見ていきます。
2.回転角度θから移動距離bの計算
さてここで、DCステッピングモーターという種類のモーターの制御を少しだけ考えてみます。DCステッピングモーターというのは直流電流のパルス信号で回転するモーターです。2相タイプと5相タイプがあり、2相タイプは1パルスで1.8°回転します。5相タイプは1パルスで0.72°回ります。実はハーフステップというものもあってこれは1パルスで0.36°回ります。
5相タイプでは、500パルスで1回転します。(500×0.72°=360°)5相パルスモーターを使ってX方向に-50㎜移動させようとすると、41.40962/0.72=57.51パルス分の回転が必要になります。実際にはパルス出力に小数点はあり得ませんので、57パルスもしくは58パルス出力となります。
このとき、回転角度は次の通りになります。
57パルス出力➡41.04°
58パルス出力➡41.76°
ではそれぞれの回転角度でのX方向の位置bを計算してみます。
計算式 b=c×cosθ
ここでθはラジアンのため、°➡ラジアンに変換します。
41.04[°]×π/180[rad]=0.716283125[rad]
ではbを計算します。
①57パルス出力のとき
b=200×cos(0.716283125)=200×0.754=150.8503≒150.9
②58パルス出力のとき
b=200×cos(0.728849)=200×0.746=149.1882≒149.2

つまりX方向の停止精度は150+0.9~-0.8になります。
もっと停止精度を良くしたい場合、ハーフパルスを使う(⇔コストアップ)、腕の長さ(c)を短くする(⇔動作範囲が小さくなる)、減速ギアを入れる(⇔回転速度が遅くなる)などの方法をあるいはそもそもステッピングモーターではない違う機構を採用することを検討します。
私の場合、スカラロボットの動作範囲を確認するときや、位置決めで回転方向にズレる可能性があるときに、三角関数には大変お世話になっております。
◆エクセルでの計算
1.角度θを算出する。
①D2セルに「=(D4^2-D3^2)^0.5」入力
②D3セルに任意の値を入力
③D4セルに任意の値を入力
④D5セルに「=D2/D3」入力
⑤D6セルに「=(ATAN((D5)))」入力
⑥D7セルに「=DEGREES(D6)」入力
2.回転角度θから移動距離bの計算
⑦D9セルに任意の値を入力。
⑧D10セルに「=RADIANS(D9)」入力
⑨D11セルに「=COS(D10)」入力
⑩D12セルに「=D4*D11」入力

CADで描けば計算せずとも角度や距離は出せますが、私は割とうっかりミスが多いのでたまに手計算で確かめるようにしています。
前のブログは ボルトの推す力は結構大きい!
次のブログは 普通公差はまず4つの数字を覚えましょう!
技術資料一覧はこちらから⇒「技術資料」
コメントをお書きください