◆アーチモーションの効果を計算しよう!
◆ロボットハンドの動線
ピック&プレイス(P&P)などを行う産業用や協働ロボットの動作にアーチモーションを取り入れると1作業のサイクルタイムが6.0秒から5.25秒に、12.5%の効率アップ!設計者ならこの12.5%を計算で出してみましょう。
自動機械でよくある部品を取って置く動作、ピック&プレイス(P&P)。アーチモーションを取り入れることで効率よく動かしましょう!割とよく聞く話です。ではそのアーチモーションの最適化はどのようにすればよいでしょうか?アーチモーションを取り入れるとA点で部品を取ってD点で部品を置くという動作の時間は短くなりますが、動作の範囲が大きくなります。アーチモーションを取り入れない場合の動線が図1、アーチモーションを取り入れた場合の動線が図2になります

図1 アーチモーションがないとき

図2 アーチモーションがあるとき
ではなぜ動線が長くなるアーチモーションの方が動作が早くなるのか?計算していきましょう。
図3に示すように移動距離をA点→B点を200㎜、B点→C点を500㎜、C点→D点を200㎜移動と想定します。
500㎜というと成人男性の肩幅くらい、200mmというと成人男性が手のひらを目一杯広げたときの親指の先端から小指の先端までくらいです。

図3 移動距離
◆アーチモーションが無いときの動線とサイクル計算
A点→B点の移動は図4に示すグラフのように加速・等速・減速を経てB点に到達、一時停止します。B点に到達したら次にB点→C点へは同じように加速・等速・減速を経て到達、一時停止します。そしてC点→D点へと移動します。
このとき、ロボットの最高移動速度が200㎜/s、加速度は0.5秒で最高速度に到達するとしたらA点からB点への移動時間は何秒になるでしょうか。
【計算式】
移動距離x(mm)
速度 v(mm/s)
加速度 a(mm/s2)
時間 t(s)
v=a・t
x=1/2 a・t^2
a=V/t
【計算】
A点→B点の移動時間を計算します。
1.加速度の計算
a= V/t =200/0.5=400mm/s2
2.加速(減速)中の移動距離計算
x=1/2 a×t^2=1/2×400×0.5^2=50mm
つまり最高速度までの加速、あるいは最高速から停止までの減速に0.5秒かかり、その間に50㎜移動します。
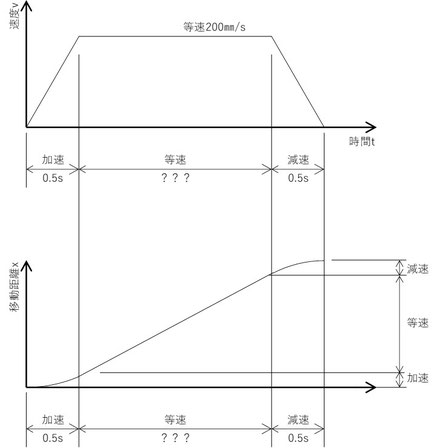
図4 加速・等速・減速の時間と移動距離
3.等速移動中の経過時間計算
A⇒Bの移動距離は図3から200mmです。加速中に50㎜、減速中に50㎜移動しますので等速区間の移動距離は100mmになります。
∴等速移動中の経過時間は100/200=0.5s となります。
加速0.5秒、等速0.5秒、減速0.5秒という計算結果になりました。
よってA点→B点への移動にかかる時間は1.5秒になります。
0.5s+0.5s+0.5s=1.5s
同様に計算をすると、
B⇒C区間は3.0sになります。
C⇒D区間は1.5sになります。
よってA⇒Dの移動時間は6.0sとなります。
◆アーチモーションがあるときの動線とサイクル計算
アーチモーションが無いときはB点停止するためその手前で減速が始まります。アーチモーションはB点で止めずにB'点まで移動させます。B点に到達した時点でC点への移動加速が始まるとともにB'に向かって減速が始まります。よってB点を最高速度で通過することができます。この差がA点→D点への到達時間の短縮に繋がります。

図5 アーチモーションがないときの動線
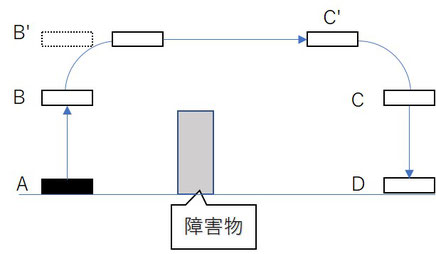
図6 アーチモーションがあるときの動線
計算で確かめましょう。
A点→B点の移動時間を計算します。
1.加速度の計算
a= V/t =200/0.5=400mm/s2
2.加速中の移動距離計算
x=1/2 a×t^2=1/2×400×0.5^2=50mm
3. 等速移動中の経過時間計算
A⇒Bの移動距離は図3から200mmです。加速中に50㎜、減速中に50㎜移動しますが減速はB点を過ぎてから始まりますので等速区間の移動距離は150mmになります。
∴等速移動中の経過時間は150/200=0.75s となります。
加速0.5秒、等速0.75秒でB点に到達します。
つまり移動開始から1.25秒でB点に到達し、C点へ向かう移動が始まります。
B点→C点の計算はC点の手前C’で減速を開始させてD点へ向かうため下方向へ加速開始します。
これを計算すると
B点→C’点は2.5秒
C’点→D点は1.5秒
A点→B点の1.25秒を合わせて
A→D点の移動は5.25秒になります。
◆計算結果、ロボットの動きが12.5%スピードアップ!
アーチモーションが無いとき ・・・ 6.0秒かかる!
アーチモーションがあるとき ・・・ 5.25秒かかる!
トータル0.75秒、12.5%のスピードアップとなった!
コメントをお書きください